量子コンピュータが実現するとどうなる？その仕組みから解説

量子コンピュータとは

量子コンピュータとは物質を構成する原子などの量子の性質を活用し処理を行うコンピュータです。「量子もつれ」や「重ね合わせ」といった量子力学現象を利用することで並列計算を可能にし、今まで以上の速度や規模で計算ができるようになりました。

量子コンピュータは、1982年にリチャード・ファインマンによって量子の動きを計算することを目的とし提案され、1985年、イギリスの物理学者ドイッチュによって計算の基礎理論がまとめられました。

以下の点が量子コンピュータを理解するポイントになります。

• 量子コンピュータでは、現代の一般的なコンピュータが情報を処理する仕組みをベースに量子の持つ性質「重ねあわせ」を利用することによって問題を速く解けるようになる。
• 今後すべてのコンピュータが量子コンピュータに置き換わるわけではない。量子コンピュータで速く解くことのできる問題は限られており、まだ使用用途も限定的なものである。
• 現代の量子コンピュータはフルスペックの量子コンピュータからはほど遠い。まだ技術的に未解決な部分も多く、フルスペックの量子コンピュータが実現できるのがいつになるのかはわからない。

量子コンピューターの原理

初めに量子コンピュータの原理である量子力学について簡単に説明します。

量子力学とは、ナノサイズ（1メートルの10億分の1）あるいはそれよりも小さな物質や、そのふるまいを扱う学問です。物理法則などが通用せず、量子は「粒であり、波でもある」というような独自のふるまい、特徴を持っています。
この奇妙なふるまいをよく表した非常に有名な実験に、二重スリットの実験というものがあります。

この実験では、板に細長い隙間を２つ開け、電子がその２つの並んだ隙間を通り抜けるときに何が起こるかを検証しました。電子が左の隙間を通れば電子は左寄りに、右の隙間をとおれば電子は右寄りにぶつかることが想定できます。

しかし、結果は電子１個を発射したところ、壁のある一点にぶつかり、もう１個発射すると今度は別の一点にぶつかります。これを繰り返していくと、電子がぶつかった位置とぶつからなかった位置が交互に現れます。これは、先に述べた予想とは大きく異なる結果です。

ここで、２つの隙間のうち右側の隙間を閉じてみると、電子は左側の隙間を通り、壁の左側にぶつかります。左側の隙間を閉じた時も同様にして壁の右側にぶつかります。つまり、”隙間が２つのときだけこのような現象が起こる”という私たちの常識からは考えられないような結果になるのです。

この不思議な結果は以下のような理解しがたい説明によって、説明づけられます。
電子は左の隙間を通った可能性と右の隙間を通った可能性があり、どちらの可能性にも確定せずに、両方の可能性を「重ねあわせた」状態になっている。２つの波を重ねあわせると干渉が起こるように、１個の電子の中で２つの可能性が重ねあわせることで干渉が起こる。
つまり、電子はどちらの隙間を通ったかの２択なのではなく、重ねあわせという状態になって両方の隙間を同時に通り抜けた。壁にぶつかる直前までは複数の場所に存在する可能性が重ね合わさっているが、壁にぶつかった瞬間に重ねあわせは壊れ、どれか１つの可能性に決まる。すなわち、”電子はぶつかる直前までは波のようにふるまっているが、ぶつかった瞬間には粒としてふるまっている”。

この「重ねあわせ具合」、つまりどのように重なりあっているのかというのが量子コンピュータの肝になります。これは水面の波が干渉しあう様子をイメージするとわかりやすいのですが、2つの隙間を通り抜けた波の「大きさの比」と「振動のタイミングのずれ」から決まります。

量子コンピュータと従来のコンピュータの違い

量子コンピュータの仕組みはどのようになっているのでしょうか？

量子コンピュータの仕組みについて説明する前に、私たちが現在使っているコンピュータについて説明します。

通常のコンピューターの仕組み

スイッチがONならば電気を通し（導通）、OFFならば電気を通さないという一般的な回路をイメージしてください。
「コンピュータの世界は0と１からなる二進数の世界である」ということは有名ですが、この０と１はビットと呼ばれ、スイッチのON/OFFで表現されています。コンピュータは、このスイッチのON/OFFを切り替えることで計算しているのです。

このスイッチはトランジスタと呼ばれるもので、電気信号を入れるとON、入れないとOFFになっており、トランジスタをつなげるとドミノ倒しのようにトランジスタのON、OFFが変化します。このようにトランジスタをつなげることで、NOTやANDなどの基本論理演算を行っています（NOTとはビットを反転させ、ANDは２つの入力がいずれも１のときのみ１を出力し、それ以外のときは０を出力する論理ゲートです）。この基本論理演算を組み合わせることで、加減乗除を行い、さらに加減乗除を組み合わせて、微分・積分、三角関数、対数関数などの複雑な計算を行っているのです。コンピュータでは、このようにトランジスタが連携することによって、複雑かつ高度な計算を全自動で行うことができます。

現代のコンピュータの脳みそである、CPU（中央演算処理装置）の部分は大量のトランジスタの集合体です。驚くべきことに、1辺数センチほどの小さいチップにトランジスタが約10億個ほど入っており、ON/OFFを１秒間に10億回ほど切り替えています。

これらのことから、CPU内のトランジスタの数はコンピュータの性能に直結しています。これまで、コンピュータは「同一面積あたりのトランジスタの数は１年半ごとに２倍になる」というムーアの法則（この法則を提唱したゴードンムーアは、米インテルの創業者の一人）によって予言されていた通りに発展してきました。黎明期と比べ、コンピュータの性能が年を追うごとに飛躍的に向上していることは実感されている方も多いと思います。しかし、近年ムーアの法則の限界が近づいていると言われています。なぜなら、トランジスタのサイズが原子１個のサイズに迫っているため、物理的にこれ以上小さいトランジスタを作ることは不可能であるという限界が見えてきたためです。そこで生まれたのが量子コンピュータなのです。

また、既存のコンピュータには消費エネルギーの問題もあります。現在のスーパーコンピュータは消費エネルギーが膨大であり、例えば、スーパーコンピュータ「京」では約3万世帯分に相当する電気量、年間約20億円もの電気代がかかっていました。量子コンピュータは一般的なコンピュータに比べると消費エネルギーが少ないと言われています。

量子コンピュータの仕組み

量子コンピュータは量子ビットという特別なビットを使って計算をします。量子ビットとは「0と1の重ねあわせ」の情報を表しており、例えば一般的なコンピュータでの「00」「01」「10」「11」の４つの状態は、量子ビットを２ビット使うことで同時に表現することができます。量子コンピュータの「量子」は英語で"Quantum"と言います。なので量子ビットのことを”Quantum Bits”、略して"Qubits"と言われます。

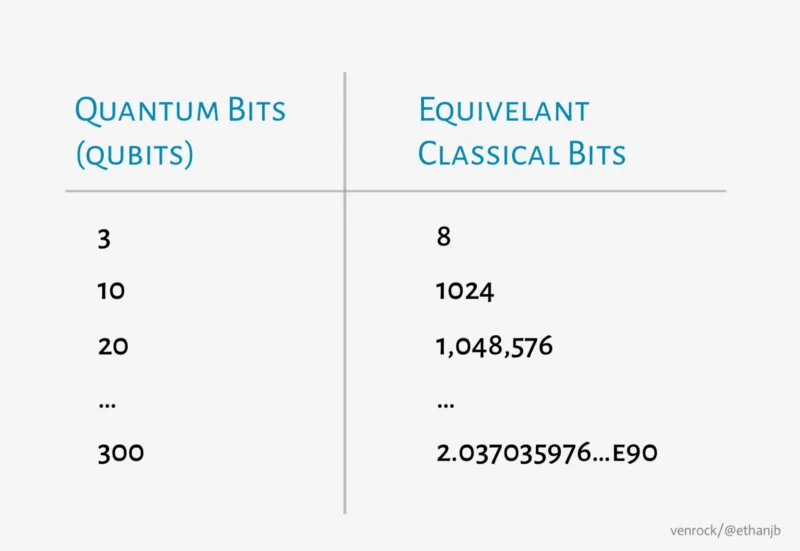
右側は今までの古典的コンピュータ、左側は量子コンピュータのそれぞれの一定の状態数を表すのに必要なビット数の比較です。量子ビットは見ての通り、古典的コンピュータに比べて指数関数的に性能が良くなるという事がわかります。

また、一般的な論理ゲートは使わず、量子版の論理ゲートによって、おおざっぱに言えば量子ビットの波の重ねあわせ具合を変えています。二重スリットの実験で壁にぶつかった瞬間に重ねあわせが壊れてどれか１つの可能性に決まったように、量子コンピュータの最後の測定では１つの答えしか読みだすことができません。そこで、量子の波の性質を使い、複数のパターンを並列に計算し、波と波をうまく干渉させて正しいパターンにだけ絞り込んでいく、ということを行っています。

現在、IBM Quantum Experience（通称IQX）によって、誰でもクラウド経由で量子コンピューターにアクセスして量子計算を実行することができます。（IQXのログインはGoogleアカウント、SNSなどから簡単に行えます）

これまでのコンピューターでは「０」と「１」のみで計算していましたが、量子コンピュータは複数のパターンででを並列で計算することで、今までよりも圧倒的に早く計算し処理することが可能になったのです。

IBM Quantum Experience. "Get started with IBM Quantum Experience". https://quantum-computing.ibm.com/docs/（IQXログインページ）

IBM developer. "IBM Quantum Experienceで体験するはじめての量子計算". https://developer.ibm.com/jp/articles/iqx-getstart/（IQXの日本語チュートリアル）

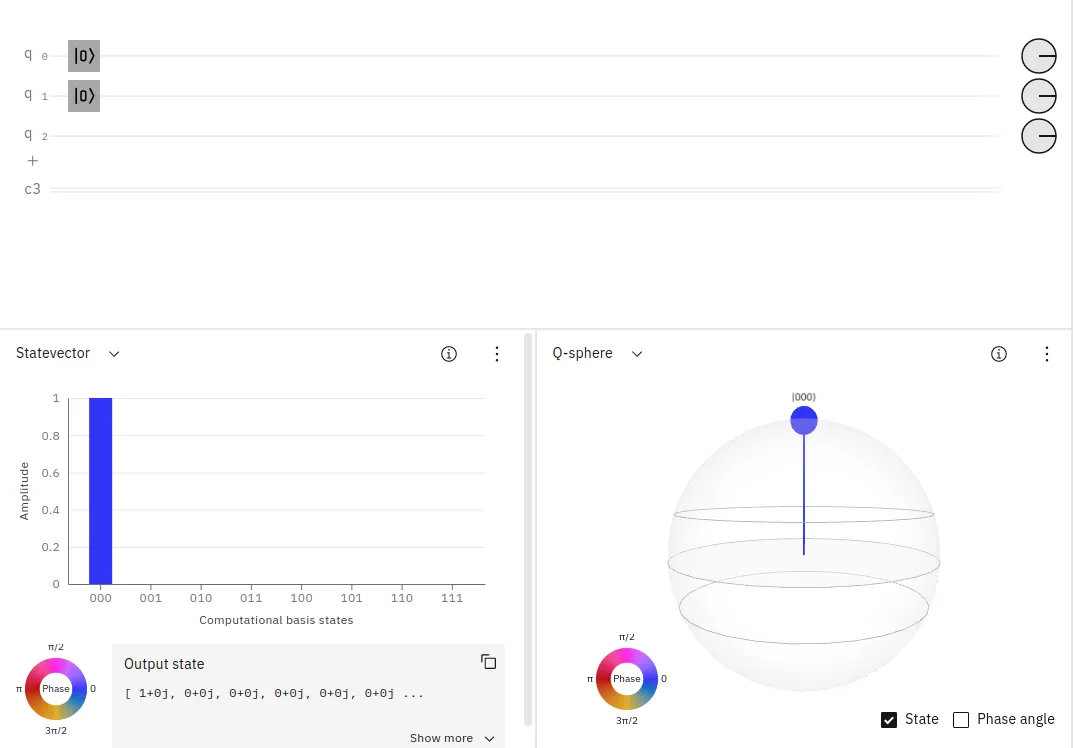
ここでは、IQXの実行結果を示し、量子版の論理ゲートの役割を視覚的に表します。

量子ビットは|0〉, |1〉というようにベクトルとして表されています。初期状態は|00〉なので、以下のように２つの量子ビットのうち最初の量子ビットq[0]にX反転ゲートを適用して測定すると、

上のような結果を得ることができます。これは、右端のビットを 0 から 1 へ反転する操作、すなわち一般的なコンピュータの論理ゲートでのNOTです。

また、量子の重ね合わせは以下のようにアダマール（H）ゲートによって実現されます。Hゲートは、X反転ゲートのように一般の論理ゲートと同じような働きをするものではなく、量子コンピュータのための特別な論理ゲートです。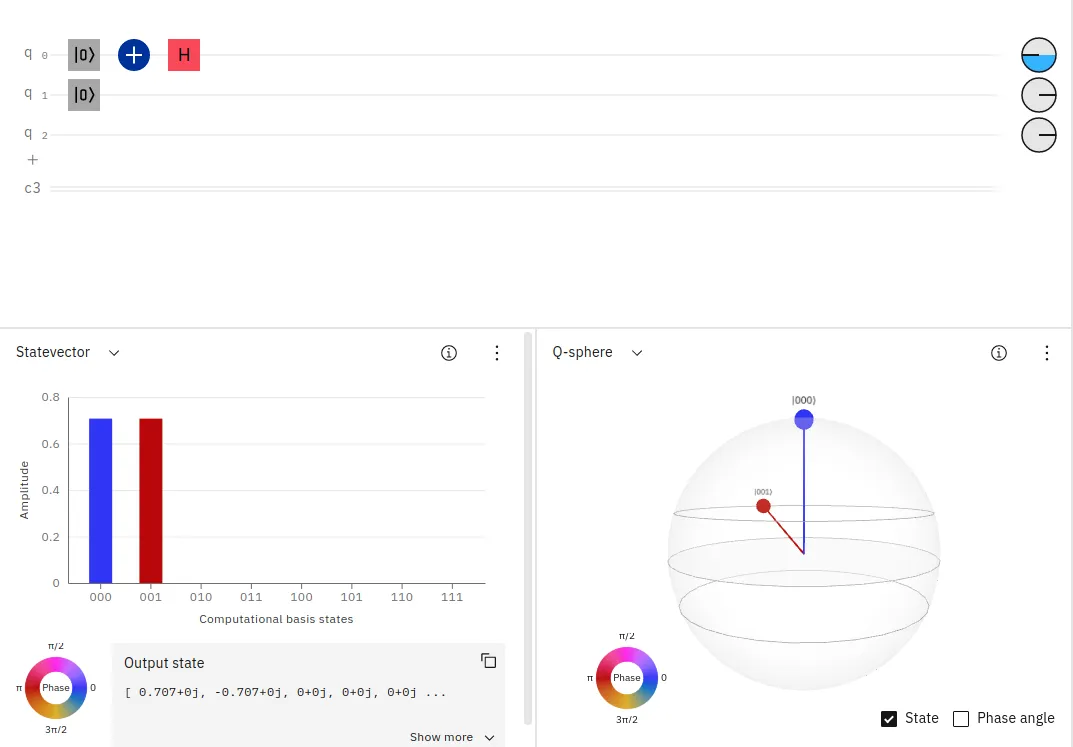

初期状態が|00〉だった２つの量子ビットのうち、最初の量子ビットq[0]にアダマール（H）ゲートを適用して測定すると、ほぼ半々の割合で|00〉と|01〉の量子状態が現れており、重ね合わせが実現されていることがわかります。

また、量子の重ね合わせだけでなく、量子もつれも実現することができます。
量子もつれとは、1つの粒子の重ね合わせが2つペアになった状態の特別な場合に起こることです。たとえば、ペアになった粒子Aと粒子Bのそれぞれのスピン（正確な表現ではないのですが、ある方向を向いた小さな矢印のようなものです）の向きが「Aが上向き・Bが下向き」と「Aが下向き・Bが上向き」との重ね合わせ状態を形成している場合を考えます。
このとき、一方の粒子を観測してその状態が分かれば、もう一方の粒子の状態は観測するまでもなく、"瞬時に"決まってしまうのです。たとえば、Aが下向きだと観測されれば、その瞬間Bは上向き状態に決まります。重ね合わせ同様、このことも私たちの常識からは考えられないことですが、量子コンピュータで実現することができます。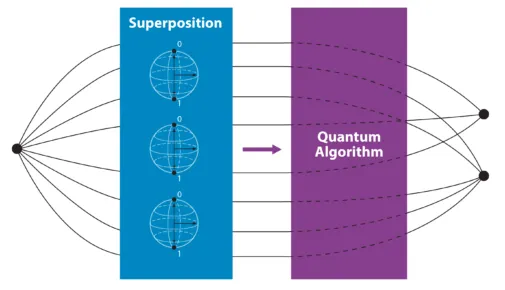

量子ビットでは一度に様々な情報が内包されていますが、受け取る時は一意に定められます。

以下のように、先ほどのHゲートを置いたあとに、入力値（小さな●）が１の時だけターゲットの量子ビット（大きな●）を反転させるCNOTゲートを適用します。

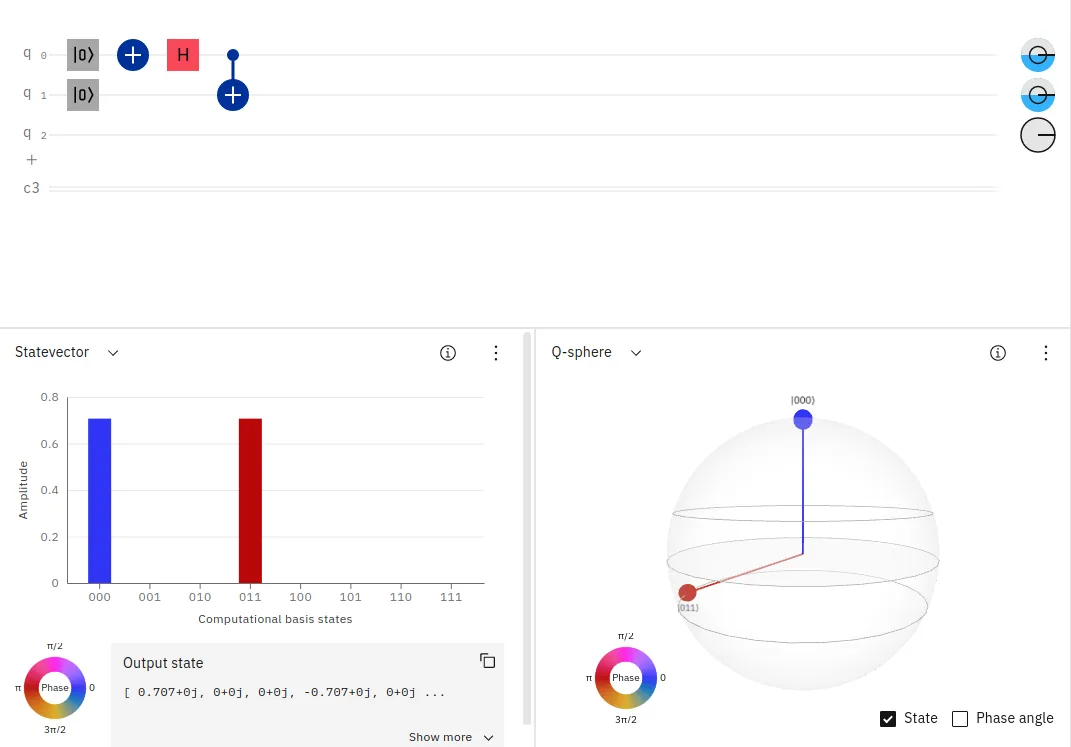
すると、上の棒グラフが示すように結果は|00〉または|11〉となります。つまり、一方の量子ビットを測定した瞬間、100%の確率でもう片方が一方の量子ビットと同じ量子状態をとることを意味しています。

これらのゲートの働きなどを応用することで、量子アルゴリズムを組むことができます。量子アルゴリズムで有名なものには、グローバーのアルゴリズム、ショアのアルゴリズムが挙げられます。
グローバーのアルゴリズムとは、探索アルゴリズムの一種です。たくさんの引き出しのある棚の中に探したいものがある状況を想像してください。
どの引き出しに探しているものがあるのか調べるのはとても手間がかかることがわかると思います。グローバーのアルゴリズムはこのように手間のかかる”探索”を効率的に行うアルゴリズムです。

また、ショアのアルゴリズムとは、素因数分解を行うアルゴリズムです。
ショアが示したのは、量子コンピュータによって 15=3×5 に素因数分解できた、という中学生にもできるような簡単なことですが、今後、量子コンピュータの性能が上がっていくことによって、もっと大きな桁数の素因数分解を行うことが期待できます。
それぞれのアルゴリズムが具体的にどのように動いているのか理解するためには、前提として数学の知識が必要となるため、ここでは説明しませんが、もっと詳しく知りたい方は、こちらのリンクが参考になるかもしれません。
Quantum Native Dojo. "Welcome to Quantum Native Dojo!". https://dojo.qulacs.org/ja/latest/index.html

また、現在、このように量子ビット、量子版の論理ゲートを実現するためのハードウェア開発が、超伝導、半導体、イオントラップ、冷却原子、光など様々な方式からのアプローチによって行われています。近年の「量子コンピュータブーム」はGoogle, IBMなどの巨大企業がこのハードウェア開発に参入したことから始まったとも言われています。どの大学、企業が、どのような方式からのアプローチを行っているのか詳しく知りたい方は、よろしければ下記のリンクを参考にしてください。

Qmedia. "量子コンピュータを実現するハードウェア（後編）". https://www.qmedia.jp/making-quantum-hardware-2/

開発されてる量子コンピュータの種類

現在、研究が進めらている量子コンピュータですが、汎用型の「量子ゲート方式」と特化型の「量子アニーリング方式」の二つが広く研究されています。

量子ゲート方式

量子ゲート方式は汎用型量子コンピュータといわれ、従来のANDゲートやORゲートなどの論理ゲートの代わりに量子ゲートを配置し、初期化、ゲート操作、測定の3ステップで計算が行われており、利点として、高速化が保証されているアルゴリズムが複数あることや設計性が高いことがあげられています。
しかし、従来のトランジスタを用いたコンピュータでは、ゲートごとに出力されノイズが除去されていたのに対して、量子ゲート方式は入力からそのゲートまでの波の重ね合わせで表現しています。そのため、量子ゲート方式はノイズに弱いとされており、「誤り」が発生しやすく、現在確立されている「誤り訂正技術」よりも優れた誤り訂正技術の開発が課題とされています。

量子アニーリング方式

量子アニーリング方式は特化型量子コンピュータと呼ばれ、イジングモデルと呼ばれる数式を解くことで、消費エネルギーが最小となる組み合わせ最適化問題の近似解を算出します。
ポートフォリオ作成など、社会課題に対して応用範囲が広いことが利点として挙げられていますが、対象となる組み合わせ問題の定式化や高速化手法が見つかっていないことなどが欠点としてあげられています。

まとめると、
・量子ゲート方式は速いが精度が悪い
・量子アニーリング方式は応用が効くが処理に時間がかかる

量子コンピュータの実用化でできること

量子コンピュータが実用化でできることは、主に2つあります。量子アニーリング方式による組み合わせの最適化と、量子ゲート方式による素因数分解の高速計算です。ここではその内容につて活用例と伴に解説します。

量子アニーリング方式による組合せの最適化

量子コンピュータが実用化されるとできることの一つとして、量子アニーリング方式による組み合わせの最適化があげられます。
「組合せ最適化問題」は、現代コンピュータの手で負えない難問としてよく紹介されます。まず、最適化問題とは、「実行可能解の中で目的関数を最適にするような問題」です。
そして、組合せ最適化問題とは、「解が順序や割当のように組合せ的な構造を持つ最適化問題」のことを言います。
組合せ最適化問題では問題のサイズに関して、実行可能解の数が指数関数的に増えていくため、実行可能解に対して全探索を行うと最適解を求めるのに天文学的な時間が必要となります。

量子コンピュータでは量子重ね合わせによる並列計算によって総当りすることができ、現代のコンピュータよりも高速に解くことが出来るのではないかと期待されています。
この方法は、Groverの検索アルゴリズムとして知られており、問題サイズを*n*とするとき、現代のコンピュータで*O(2^n)*の計算が必要な問題でも、量子コンピュータならば*O(2^(n/2))*の計算で済みます。
指数部分が半分になるだけでもだいぶ高速に解くことが出来るようになります。ただ、問題のサイズが大きくなれば、天文学的な時間がかかることには変わりはないので、得意であると言い切ることは出来ませんが、今まで膨大な計算時間によって断念していた問題やアルゴリズムの一部に関してさらなる研究成果が出ることが期待されています。

自動運転

組み合わせの最適化の応用例として自動運転があります。自動車の自動運転には、どのルートを回るのかを判断する必要があります。こういった場面でも量子コンピュータは大いに役立ちます。その際に使われるのが”組合せ最適化問題”です。膨大なルートの組み合わせからどれが一番最短かを計算してはじき出し、ルートを設定、車を制御します。

新薬の開発

組み合わせの最適化の応用例として新薬の開発もあります。新薬の開発に膨大な種類の組み合わせから最適なものを導き出す必要があります。この際にも組み合わせ最適化が役立ち膨大な種類の組み合わせから最適な組み合わせを選定することができます。

量子ゲート方式による素因数分解の高速計算

量子コンピュータが実現すると、量子ゲート方式により素因数分解を用いて高速で計算できます。1994年、ピータ・ショアが量子コンピュータを用いた素因数分解の解法を発見しました。このように以前から素因数分解の解法は見つかっていましたが、量子コンピュータの実現により計算の高速化が可能になります。

暗号解読

素因数分解の高速計算の応用例として暗号解読があります。量子コンピュータが実現すると、従来のコンピュータのインターネットのセキュリティや金融機関での暗号が容易に突破できます。
現在のあらゆるインターネット通信に使われる暗号化の方式であるRSA暗号は、巨大な数の素因数分解は極めて困難であるという前提に基づいて作られています。

つまり、量子コンピュータによって高速に巨大な数を素因数分解することが可能になってしまえば、現在使われているRSA暗号は破られてしまうということです。
量子コンピュータによって、RSA暗号に変わる新たな暗号（おそらく素因数分解に頼らない暗号）を作る必要が出てきています。
その他、"Quantum Algorithm Zoo"（https://quantumalgorithmzoo.org/）というHPに量子コンピュータで高速化できる計算がまとめられています。

量子コンピュータでの機械学習

ここでは、量子コンピュータを使用して機械学習を行う、量子機械学習についてのお話をします。

量子機械学習のアルゴリズムは古典的モデルをベースに考えられていることが多いです。
量子機械学習は量子データとハイブリッド量子古典モデルの2つの概念を元にして構築されています。
自然または人口に量子のシステムで発生したすべてのデータソースのことを量子データと呼びます。量子データは重ね合わせと絡み合いを示します。

量子計算と機械学習を組み合わせてアプローチは4つに分かれます。量子がQ(Quantum)で、古典がC(Classic)です。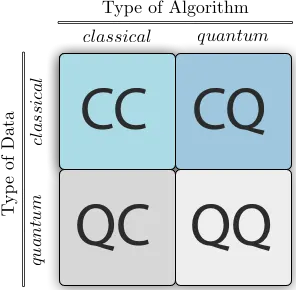

CCアプローチは従来の古典コンピュータで機械学習をすることを指します。機械学習や深層学習について振り返ってみたいという人は是非以下の記事を見てみてください。

>>機械学習とは?概要やアルゴリズムを詳しく解説!

>>深層学習について詳しく説明！

QCアプローチでは、機械学習が量子計算にどのように役立つかを確認します。量子コンピュータの内部の観測データーを機械学習することで、量子コンピュータの内部状況を理解できたり、量子コンピュータの開発に役立つことができます。

CQアプローチでは、テキスト、画像などを古典系の観測値で捉え、分析に量子コンピュータを用いることです。量子コンピュータでのアルゴリズムが使用されています。

QQアプローチでは量子コンピュータによって処理される量子データを扱います。量子状態のすべての情報を測定するためには、指数関数のスケールの回数の測定を必要とするが、量子コンピュータでは即座にすべての情報にアクセスすることができ、即座に判断を行うことができます。これがQQの強みです。QQは完成すれば素晴らしいテクノロジーとなることは間違いないのですが、現状では研究成果が乏しいです。

現状量子機械学習と呼ぶ時、QQとCQのことを指すことが多いです。先程述べたようにQQのほうは実用性に乏しく、教師あり学習のCQアプローチが現在では注目されております。

量子機械学習の活用例として、新しい素粒子の発見が出来ると言われています。

AWSで量子コンピュータ

AWSで量子コンピュータを使用できることについて説明をします。

まず最初にAWSについてざっくり説明します。AWSとはAmazon Web Servicesの略称です。Amazon社が提供しているものとなっています。AWSでは、クラウドコンピューティングのサービスを行っています。クラウドコンピューティングとは、インターネットを介せば、手元にあるコンピュータを使用すうときに、大量のストレージ、高速なデータベースを必要なだけ利用することができます。要は、実質無制限の容量などを持つものに接続できることということです。

Amazon社はAmazon Braketと呼ばれる、量子コンピューティングを提供しています。

AWSで使える量子コンピュータ

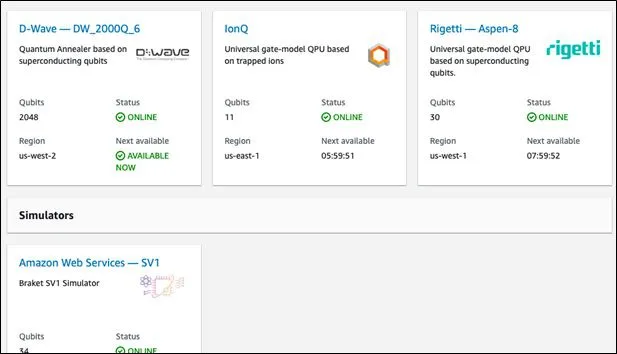
Amazon Braketでは、複数の量子コンピューターを使いクラウド経由で量子計算ができるサービスのことです。カナダのディーウエーブシステムズ（D-Wave Systems）、米IonQ（イオンQ）、米リゲッティ・コンピューティング（Rigetti Computing）の量子コンピューターをクラウド経由で利用することができます。目的に応じて方式の異なる量子コンピュータを利用することができます。

D-Waveではアニーリング式が、IonQではイオン化したイッテルビウム原子を用いた汎用性のあるゲートベース、Rigettiでは、 超伝導量子ビットをベースとした汎用性のあるゲートベースのマシンです。

量子コンピュータのプログラミングを学んだり、自分自身で量子アルゴリズムを作成したりすることもできます。

AWS 無料利用枠を利用することで、1 年間の Amazon Braket シミュレータの実践的経験を得ることができるので、登録がまだの方はこの機会に登録をしましょう。

Amazon Braket ソフトウェア開発キット (SDK) とよばれる、テクノロジーに依存しないデベロッパーフレームワークがあり、これを利用します。

量子ビットアクセス：有料量子コンピューティング

Amazon BraketではSageMakerのJupyter Notebook環境を構築することができて、このJupyter Notebook環境にはというgithub.com/aws/amazon-braket-sdk-python/フレームワークが予めセットアップされており、このSDKによってAmazon Braketの様々な量子コンピューターをPythonから操作できるようになっています。

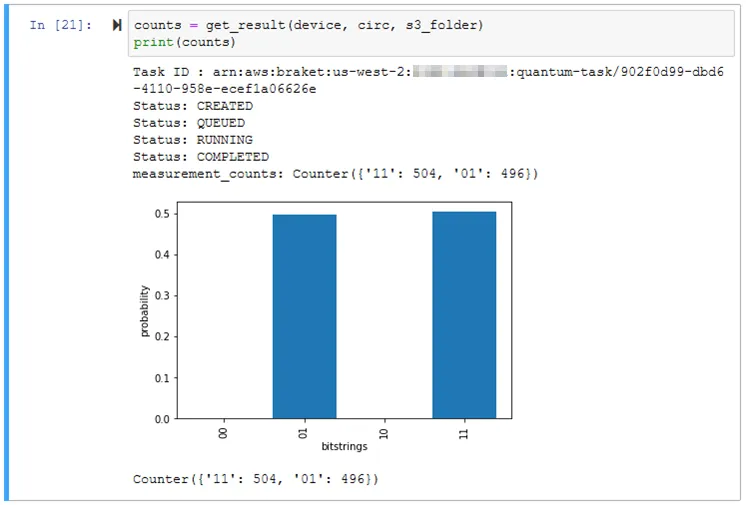
AWS量子コンピュータでjupyter

したがって開発者はJupyter Notebook上で、Amazon Braketの量子コンピューターを使えるということになります。

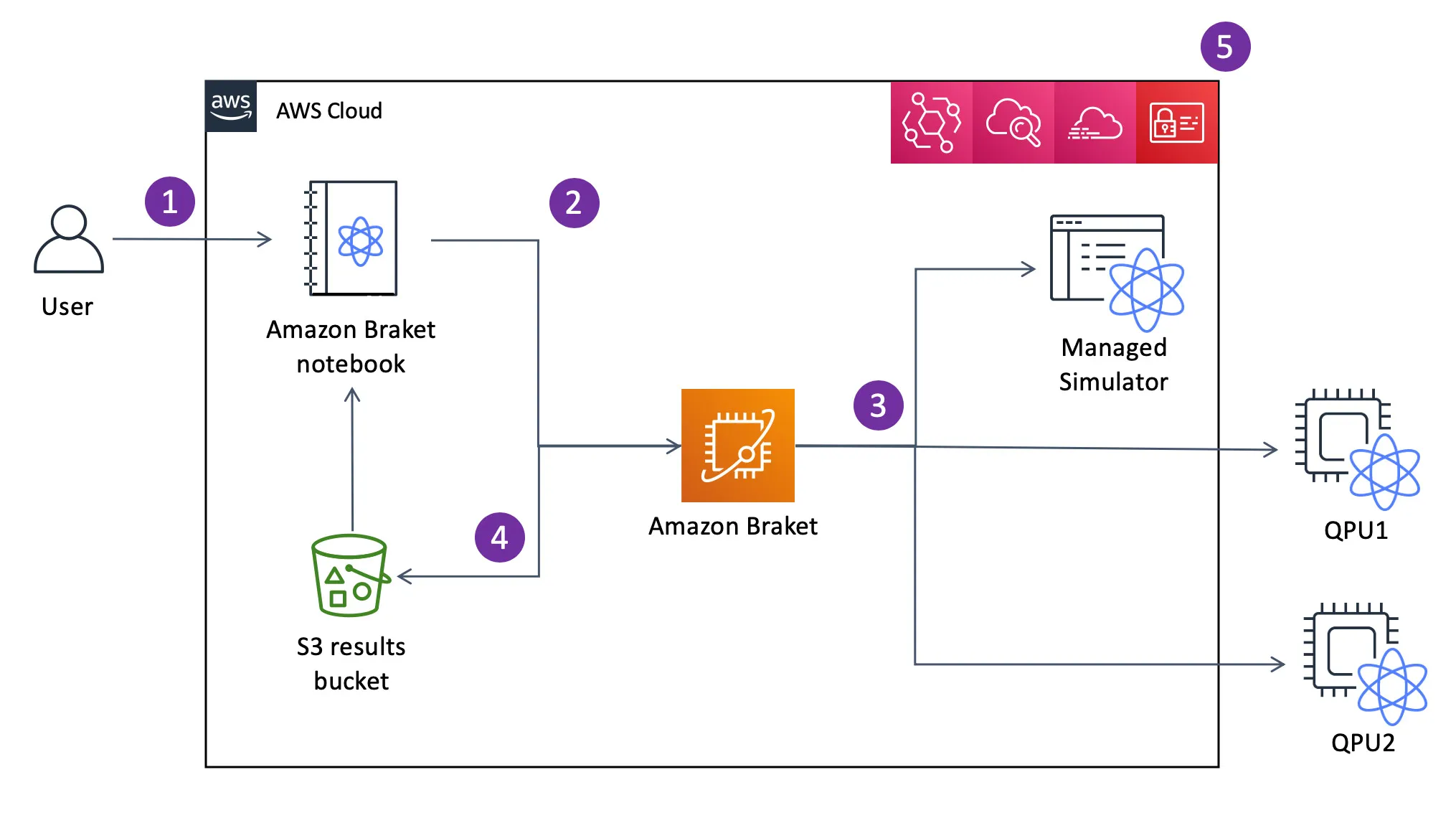
Amazon Braketの仕組み

（Amazon Braket タスクフロー）

費用がそれぞれ異なるので使う際は目的の用途に応じて値段を確認して使用しましょう。

量子コンピュータを扱う会社は日本にも存在します。
↓詳しくはこちら
日本で量子コンピュータを開発する企業の事例

量子コンピュータがもつ未来への可能性

ここまでおおまかではありますが、量子コンピュータについて解説してきました。

今回、基本的には文章での説明を試みましたが、量子力学の世界はとても抽象的なので、文章にしようとすると不正確な表現になってしまいがちであり、実際には量子コンピュータについての基本的なことを理解するためには数式が不可欠です。
そして、量子コンピュータは今日本でも様々な企業によって開発されており、将来様々な分野でその実用化が期待され、ビジネスの観点でも重要になる技術です。この記事では、量子コンピュータについてほんの一部しか説明できていませんが、量子コンピュータについて興味を持つきっかけになれば幸いです。

2022年世界中のメディアで量子コンピュータが話題になりました。2023年も大規模な研究開発結果の発表を楽しみにしましょう。

この記事を読んで興味を持っていただいて、弊社での開発取り組みを気になった方は是非以下のSNSもご覧頂けると幸いです。

Twitter https://twitter.com/crystal_hal3
Facebook https://www.facebook.com/クリスタルメソッド株式会社-100971778872865/

［関連記事］
量子コンピュータはシンギュラリティの実現に近づけるか。量子理論によってコンピュータの計算能力は大きく進歩しました。それによってシンギュラリティ―技術的特異点―は確実に実現に近づきました。ではいつ実現するのか？2045年問題とは？以下の記事でイチから解説します！是非ご覧ください！
>> シンギュラリティとは？意味やいつ起こるのか解説